
Objectifs de l’enseignement : Comprendre les civilisations et l’évolution de l’esprit mathématique à travers les âges.
Connaissances préalables recommandées : Culture générale et scientifique.
Contenu de la matière :
Chapitre 1 : Introduction.
Chapitre 2 : Les origines.
Chapitre 3 : Les Mathématiques Babyloniennes.
Chapitre 4 : Les Mathématiques de l’Egypte ancienne.
Chapitre 5 : Les Mathématiques Grecques, Hellénistiques et Romaines.
Chapitre 6 : Les Mathématiques en orient musulman et en occident musulman.
Chapitre 7 : La transmission du savoir mathématique vers l’Europe.
Chapitre 8 : La renaissance en Europe.
Chapitre 9 : La révolution industrielle et ses conséquences.
Chapitre 10 : Le 19ème siècle et la crise des fondements.
Chapitre 11 : Le 20ème siècle et l’élargissement du champ d’application.
- Enseignant: BARKAT Omar

- Enseignant: MILLES Soheyb

Acquérir les éléments fondamentaux de l’algèbre à savoir les espaces vectoriels, algèbre multilinéaire et la réduction des endomorphismes.
- Enseignant: BARKAT Omar
Contenu de la matière:
Chapitre 1 : Prise en Main
Chapitre 2 : Les nombre en Matlab avec licence ou Scilab
Chapitre 3 : Vecteurs et Matrices
Chapitre 4 : Eléments de programmation
Chapitre 5 : Polynômes
Chapitre 6 : Graphisme en Matlab avec licence ou Scilab
Chapitre 7 :Calcul symbolique
- Enseignant: MERAHI Warda
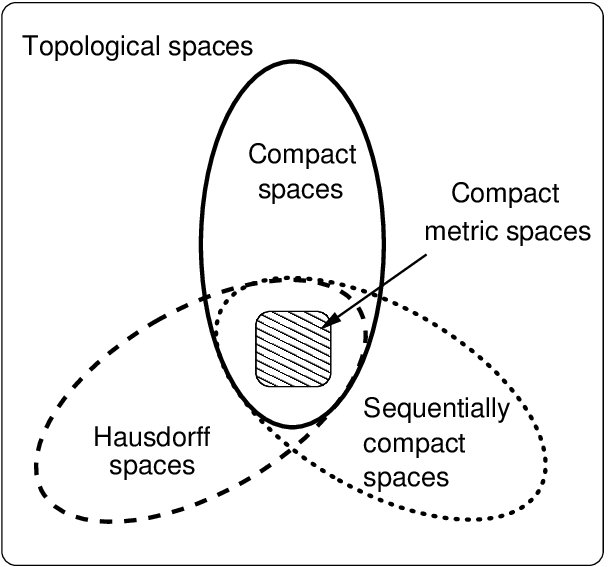
La topologie est une notion fondamentale en analyse et même en mathématiques en général. Beaucoup d’autres notions sont liées à elle, on citera par exemple les notions de continuité, de convergence,...
Ce cours a pour but d’introduire les notions générales que l’on peut définir
à partir d’une topologie et de présenter des généralités sur les espaces topologiques, toutes les définitions et propriétés doivent être parfaitement connues. des cas particuliers importants d’espaces topologiques seront étudiés en détail : les espaces métriques dans le chapitre 1, qui font intervenir la notion de distance, et les espaces vectoriels normés dans le chapitre 5, qui sont des espaces métriques particuliers .
- Enseignant: MERAHI Warda

Objectifs de l’enseignement :
Initier les étudiants aux différentes méthodes numériques sur l'approximation de fonctions et leur application dans le domaine du calcul scientifique sous MATLAB.
