Géométrie différentielle
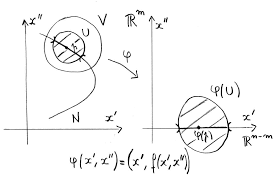
La géométrie différentielle étudie certains objets géométriques (courbes, surfaces, variétés différentiables) avec les outils du calcul différentiel. La géométrie différentielle est un domaine très important, qui a beaucoup d’applications en physique théorique (notamment dans la théorie de la relativité) et beaucoup d’interférences avec d’autres disciplines mathématiques modernes (par exemple la topologie, l’analyse, la géométrie algébrique et complexe)
introduction à la théorie des opérateurs linéaires
Familiariser l’étudiant avec les notions de base de la théorie des opérateurs linéaires pour constituer un socle
à de futures éventuelles études en EDP , en théorie spectrale et en équations différentielles abstraites
Connaissances préalables recommandées : Topologie des espaces métriques, des espaces vectoriels normés
et analyse hilbertienne
Introduction à la théorie des groupes
Ce module introduit des notions fondamentales pour la théorie des groupes, la structure de groupe est utile pour la compréhension des corps et les codes linéaires ainsi que leurs applications.
Transformations intégrales dans les espaces Lp
Un espace Lp est un espace vectoriel de classes des fonctions dont la puissance d’exposant
p est intégrable au sens de Lebesgue, où p est un nombre réel strictement positif. Le
passage à la limite de l’exposant aboutit à la construction des espaces L1 des fonctions
bornées. Les espaces Lp sont appelés espaces de Lebesgue.
Cet espace constituent un outil fondamental de l’analyse fonctionnelle en permettant
la résolution d’équations par approximation avec des solutions non nécessairement dérivables
ni même continues.